Quantification

Pour réduire le coût de réalisation des équipements de traitement, on est conduit à représenter les échantillons des signaux par des nombres entiers ayant un faible nombre de bits. Il est donc utile, pour dimensionner les chemins de données, de savoir prédire les erreurs occasionnées par la quantification ainsi effectuée.

Dans le cas d'un filtre linéaire, cette quantification pourra affecter les coefficients ou les données.

L'opération de quantification transforme une grandeur continue en une grandeur qui ne peut prendre qu'un nombre fini de valeurs Cette opération est effectuée par le convertisseur Analogique Numérique. En informatique, une fonction équivalente est la fonction de conversion entre un "réel" et un nombre "entier". 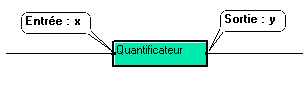Cette transformation est caractérisée par le pas de quantification qui est la largueur, exprimée en unité de l'entrée (par exemple des volts) des marches d'escalier de la caractéristique de conversion.

Soit l'erreur de quantification. On voit que cette fonction a l'allure d'une dent de scie.

Considérons que l'entrée de l'opérateur de quantification comme une variable aléatoire de densité de probabilité . La densité de probabilité de l'erreur est obtenue par un repliement de sur une largeur égale au pas de quantification. Si on suppose cette densité lentement variable devant la largeur du pas de quantification, on voit que la densité de probabilité de l'erreur devient une constante sur cette largeur.

La valeur moyenne de cette erreur dépend de la forme de la quantification. Cette quantification est généralement faite par un convertisseur Analogique Numérique : il est alors possible de régler la composante continue analogique de façon à annuler cette erreur moyenne.

Dans tous les cas l'écart type de cette erreur sera :

En prenant comme majorant de l'erreur, on peut facilement trouver un majorant de l'erreur de sortie d'un filtre, mais cette méthode de calcul et très pessimiste.

On peut utiliser le modèle statistique de l'erreur de quantification en considérant les coefficients comme des variables aléatoires. On calcule ainsi une erreur moyenne sur tous les filtres réalisables.

En fait, dans beaucoup de cas, les coefficients des filtres sont complètement connus. Il est donc possible de calculer exactement (sur un ordinateur) l'erreur introduite par la quantification sur le gain du filtre a chaque fréquence. Les calculs de majorants ou le calcul statistique ne sont alors utiles que pour un dimensionnement préalable grossier ou dans le cas des filtres auto-adaptatifs.

Une autre façon d'aborder le problème, pour les filtres de type RII (récursifs), est d'observer quelles sont les positions possibles des pôles (ou des zéros) d'une cellule de filtre. On les trouve sur un quadrillage courbe dont le pas dépend du pas de quantification des coefficients. Il se peut alors qu'il n'existe aucune position suffisamment proche de la position souhaitée et que l'erreur commise sur la réponse du filtre obtenue soit inacceptable. Il se peut même que le filtre devienne instable.

On modélise l'erreur de quantification due au convertisseur analogique numérique par un bruit additif.

<==>

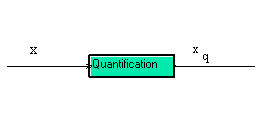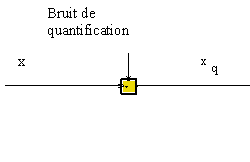
Comme on l'a montré précédemment, la densité de probabilité de ce bruit est une constante sur un intervalle de largeur , à condition toutefois que celle du signal soit relativement "douce". (Ce n'est pas le cas, en particulier si le signal est binaire ! ).

On fait généralement deux hypothèses sur ce bruit, qu'il faut discuter.

La première est que ce bruit est blanc. Il est facile de trouver des contre exemples, comme celui ou le signal d'entré est carré. Malgré cela, cette hypothèse est souvent vérifiée.

La seconde est que ce bruit est indépendant du signal d'entrée. Cette hypothèse est évidemment fausse, puisqu'il existe une transformation certaine entre les deux ! On peut néanmoins comprendre que compte tenu de la transformation qui relie l'entrée à l'erreur, cette erreur dépend de détails très petits du signal d'entrée, qui sont de faible importance.

Ce n'est que si ces hypothèses sont vérifiées que l'on peut faire les calculs de propagation de l'erreur dans les filtres. Il faut donc avoir à l'esprit, quant on en utilise les résultats, que ces hypothèses sont peut-être fausses.

Il suffit de faire le rapport entre la puissance du signal et celle du bruit de quantification.

On sait que celle de ce bruit est

On est censé connaître celle du signal, donc le problème semble trivial. La difficulté est en pratique de mettre le signal à l'échelle, ce qui revient à définir .

Il faut connaître le nombre de bits du convertisseur et sa dynamique d'entrée (tension d'entrée, que l'on supposera symétrique autour de zéro). On suppose pouvoir régler la valeur maximum prise par le signal d'entrée sur cette dynamique.

On obtient alors

Comme on vient de le voir :

  est équivaltent à :

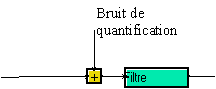
On utilise la propriété de linéarité. Filtrer la somme du bruit de quantification et du signal est équivalent à sommer les filtrées du bruit et du signal.

Il faut donc calculer la puissance du bruit de quantification propagé dans le filtre.

Cela est simplifié par l'hypothèse de bruit blanc.

La sortie d'un filtre peut être calculée par la convolution du signal d'entré et de la réponse impulsionnelle du filtre.

est donc la somme pondérée de variables aléatoires qui sont les échantillons retardé de bruit de quantification. L'hypothèse de blancheur se traduit par l'indépendance de ces échantillons. La variance de la somme est donc la somme des variances. La variance du bruit de quantification ramené en sortie du filtre est donc

Dans le cas de filtre de type passe-bande, il est plus facile de raisonner dans le domaine des fréquences.

L'équation du filtrage s'écrit alors

Si est la fonction de transfert du filtre, la Densité Spectrale de Puissance(DSP) du bruit en sortie s'écrit

La variance du bruit est l'intégrale de la DSP sur un intervalle 1. (Le signal étant discret la DSP, comme la TFd, est périodique de période 1).

Or la densité Spectrale du Bruit de Quantification est une constante. Et si l'on suppose que le filtre est un filtre passe-bas de largueur de fréquence de coupure en fréquence vrai, soit : en fréquence réduite.

et

donc

On voit donc qu'un filtrage passe-bas diminue la puissance du bruit. Il peut donc être intéressant d'utiliser un convertisseur analogique numérique fonctionnant à une cadence plus élevée que nécessaire et d'effectuer une décimation ensuite (voir filtrage multi-cadence) : on obtient ainsi l'équivalent d'une augmentation du nombre de bits du convertisseur. Attention cependant à s'assurer de la validité de l' hypothèses de bruits blanc. Il est possible d'ajouter un léger bruit avant la conversion pour cela.