le signal d'entrée d'un filtre, 
la sortie correspondante, et 
la réponse impulsionnelle de ce filtre.Soient le signal d'entrée d'un filtre, la sortie correspondante, et la réponse impulsionnelle de ce filtre.
On a vu que :
En calculant la TZ des deux membres :
|
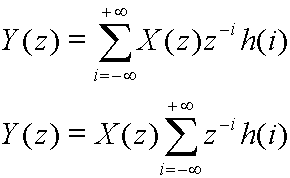
La produit de convolution se transforme en un produit simple par transformée en Z |
|
|
est appelée "fonction de transfert" du filtre.
En posant 
, on obtient 
, appelé gain complexe, qui est le gain du filtre en fonction de la fréquence 
.
Nous avons vu qu'un filtre RIF était réalisable à partir de l'équation de convolution qui comporte alors un nombre fini de termes.
Dans les cas ou cette réponse impulsionnelle est infinie(RII), on peut se placer dans les cas où la fonction de transfert factorisée possède, elle, un nombre fini de pôles et de zéros :
Calculons la TZ inverse:
On obtient une équation aux différences d'ordre fini.
En supposant 
on obtient une équation calculable par itération :
|
|
Nous savons donc réaliser un filtre à réponse impulsionnelle infinie !
Il est pratique de représenter les équations aux différences sous forme graphique, à l'aide d'opérateurs de base.
|
Retard |
|
|
addition |
|
|
Multiplication par une constante |
ou
|
Ce diagramme de flux n'est avant tout qu'une représentation graphique de l'équation mathématique. Il peut aussi être un schéma de réalisation puisque tous les opérateurs qui le constituent sont réalisables électroniquement. En fait, la réalisation sera généralement différente en raison de contrainte de vitesse ou d'économie de matériel. Ce diagramme est en particulier un bon moyen d'étudier la sensibilité du filtre aux erreurs d'arrondis.
Un filtre peut être décrit par :
On obtient immédiatement la structure de base des filtres à réponse impulsionnelle finie en transposant l'équation de convolution avec la notation du diagramme de flux.
que l'on peut noter
Cette structure est appelée "structure transversale". Elle est composée d'une ligne à retard (la chaîne des opérateurs 
) et de pondération sur les prises d'information de cette ligne.
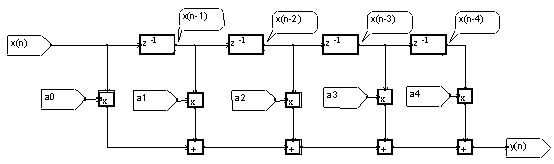
Figure 6 : Illustration du fonctionnement d'un filtre "transversal"
Cette structure de base est aussi appelée structure directe. En permutant les retards et les gains, on obtient la structure duale, fonctionnellement équivalente, mais qui peut être mieux adaptée à une mise en œuvre matérielle.
Il est à noter que ces diagrammes ne contiennent pas de boucle.
De la même façon la transposition de l'équation aux différences finies :
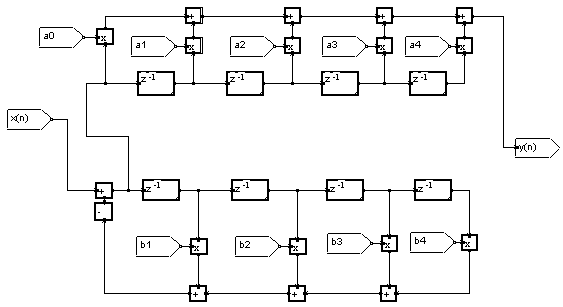
donne le diagramme de flux :
On peut décomposer ce diagramme en deux filtres en cascade. En haut, un filtre à réponse impulsionnelle finie ou "MA" pour Moyenne Ajustée. En bas, un filtre que l'on peut qualifier de "purement récursif" ou "AR" pour Auto Régressif. L'ensemble du filtre est qualifié de "ARMA". On remarque la présence d'une boucle dans ce diagramme : le calcul d'un échantillon de la sortie utilise les valeurs passées de cette même sortie.
On peut les rattacher à leur fonction de transfert. Si on note la fonction de transfert globale
Le filtre du haut correspond à
et celui du bas à
Sachant que
on peut permuter les deux filtres.
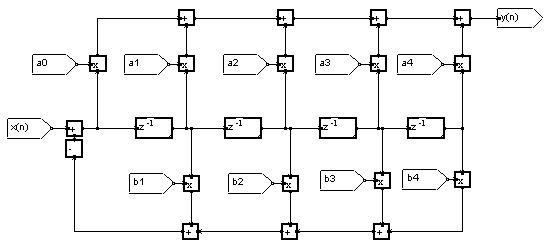
On constate alors que les deux lignes à retard mémorisent les mêmes valeurs. Il suffit d'en conserver une seule. On obtient une structure contenant le minimum de mémoires.
En fait cette structure est assez exigeante en précision de calcul dès que l'ordre du filtre est un peu grand. On préfère alors factoriser la fonction de transfert pour la mettre sous la forme d'un produit de fraction rationnelle d'ordre 2. On obtient alors une structure composée d'une cascade de filtres d'ordre 2, chacun étant réalisé selon la structure ci-dessus.
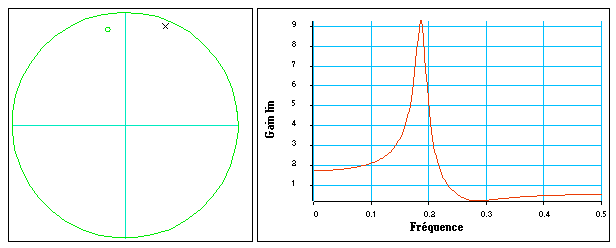
Figure 7 : Réponse d'une cellule de filtre d'ordre 2 défini par son pôle et son zéro
Soient deux filtres définis par leurs réponses impulsionnelles :
Pour chacun de ces deux filtres :
Figure 8 : Tracé des réponses de divers filtres
