Les traitements effectués sur les signaux modifient souvent leur bande passante. Si l'on veut toujours avoir une fréquence d'échantillonnage proche de la fréquence de Shannon, pour réduire le volume de stockage et le coût en calcul, il faut faire varier cette fréquence d'échantillonnage.
En entrée et en sortie d'une chaîne de traitement, on peut transférer une partie de la complexité du filtre analogique vers le numérique. On échantillonne à une fréquence relativement haute puis, après un filtrage passe-bas on revient à la fréquence d'échantillonnage voulue.
Si on sous-échantillonne la sortie d'un filtre numérique, en "sautant" des échantillons du signal, on devine que l'opération n'est pas optimale en volume de calcul puisque le filtre a calculé des échantillons qui sont ensuite supprimés. Nous verrons comment faire cette opération de façon économique en calcul.
On est souvent conduit à une réduction de la fréquence d'échantillonnage : on parle alors d'opération de décimation. Dans d'autre cas il faut augmenter cette fréquence : on parle alors d'interpolation.
Le facteur de décimation ou d'interpolation peut être entier et connu à la conception du système. Dans certains cas, il sera quelconque ou même variable au cours du temps.
Pour respecter les conditions de Shannon, il faut normalement faire précéder l'échantillonnage d'un filtre analogique "anti-repliement". Ce filtre doit être d'autant plus raide (et donc cher) que l'on souhaite approcher la limite de Shannon. Pour simplifier ce filtre, on peut choisir de s'éloigner de cette limite en augmentant la fréquence d'échantillonnage.
Il est ensuite possible d'effectuer un filtrage passe-bas numérique suivi d'un sous-échantillonnage pour se retrouver près de la limite.
Figure 33 : Illustration de la technique de conversion avec filtrage multi-cadence.
Le signal est une sinusoïde de fréquence 35 Hertz, additionné d'un bruit très large bande. La technique de conversion traditionnelle (courbes du bas) nécessite un filtre analogique raide (15 Hz de transition), alors qu'en suréchantillonnant d'un facteur 5, un filtre très doux suffit ((500 Hz de transition) : Le filtrage raide est fait par le filtre numérique. Le filtre analogique est d'autant plus doux que l'on peut accepter un repliement de spectre limité à la bande supprimée par le filtre numérique.
On a vu que la transformée de Fourier discrète (TFD) d'une série de N échantillons d'un signal est composée de N valeurs, et que l'étendue de cette transformée est égale à la fréquence d'échantillonnage. Tronquer cette transformée revient à abaisser la fréquence d'échantillonnage dans le rapport des nombres d'échantillons. On comprend que cette opération ( à la différence du simple sous-échantillonnage) comporte un filtre passe-bas puisqu'on a ainsi supprimé les composantes hautes fréquences. Il convient de prendre garde à ce que ce soient bien les composantes basses fréquences qui soient gardées : les basses fréquences négatives sont généralement placées près des derniers points de TFD.
Notons que si l'on se contente de supprimer les valeurs de fréquences hautes, l'opération de filtrage n'est pas très bonne. Il sera préférable de synthétiser un filtre de caractéristiques souhaitées et de l'appliquer dans le domaine des fréquences sous la forme d'une pondération des échantillons conservés.
Figure 34 : Réduction de fréquence d'échantillonnage par TFD.
De la même façon, on a vu dans un chapitre précédent qu'une interpolation peut être réalisée en ajoutant des valeurs nulles en hautes fréquences.
La réalisation par TFD de décimateurs ou d'interpolateurs capables de fonctionner sur des signaux longs ou même infinis peut se faire par des structures très semblables à celles qui réalisent un filtre RIF par TFD. On découpe le signal en blocs. On fait la TFD d'une suite de deux blocs. Après avoir multiplié cette transformée par les coefficients du filtre en fréquence, on tronque les hautes fréquences (pour le décimateur) avant d'effectuer la TFD inverse. On obtient naturellement en fin des blocs plus petits (ou plus grands dans le cas de l'interpolateur).
Notons que l'on pourrait être tenté de ne pas utiliser de coefficients de filtre et de seulement faire la troncation. En fait, ce filtrage brutal ( filtrage "à la hache"), qui peut être tolérable dans la cas de TFD sur tout le signal, introduit de fortes ondulations sur la réponse en fréquence et il est souhaitable synthétiser un filtre correct (Voir chapitre sur la synthèse des filtres)
On peut voir que cette méthode n'est pas optimale en coût de calcul, puisqu'on calcule des valeurs de TFD qui ne sont pas conservées ensuite. L'efficacité des algorithmes de calcul rapide de TFD ("FFT") compense cela, sauf pour de très forts facteurs de réduction.
Pour réduire la fréquence d'échantillonnage dans le rapport 
il suffit de ne garder qu'un point sur 
des échantillons de sortie. C'est une opération que l'on peut comparer à l'échantillonnage d'un signal continu et que l'on peut nommer "sous-échantillonnage". De même que pour l'échantillonnage de signaux continus, il faut généralement faire précéder de sous-échantillonnage d'un filtre passe-bas anti-repliement (ici numérique).
Supposons ce filtrage passe-bas réalisé par un filtre à réponse impulsionnelle finie (RIF) sous la forme "transverse".
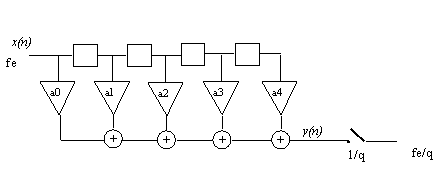
Il est bien entendu inutile de calculer les échantillons de sorties non utilisés. On peut donc placer le sous échantillonnage avant les multiplications.
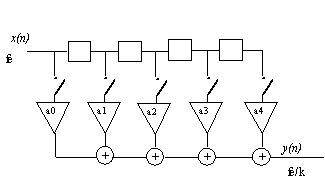
La quantité de calcul nécessaire est alors réduite du facteur . Cela permet d'utiliser des opérateurs de calculs plus lents ou en moins grand nombre.
Il est important de noter que seul un filtre de type RIF permet cette économie de calcul. Le structure nécessairement récursive d'un filtre RII, impose de calculer tous les échantillons.
Nous venons de voir que de la décimation était réalisée par un filtrage suivie d'un sous-échantillonnage.
A l'inverse, l'interpolation d'un facteur 
est réalisée par une augmentation de la fréquence d'échantillonnage (par insertion de 
valeurs nulles entre chaque échantillons), que l'on pourra nommer "sur-échantillonnage". Cette opération est suivie d'un filtre passe-bas interpolateur. On peut également comparer cela à la conversion
Supposons encore le filtrage passe-bas réalisé par un filtre à réponse impulsionnelle finie (RIF) sous la forme "transverse".
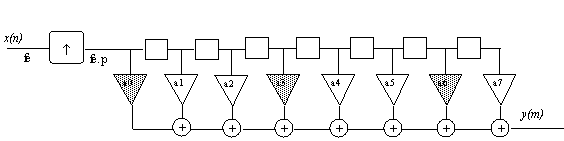
A chaque instant, seuls 
des multiplieurs opèrent sur des données non nulles. On peut alors remplacer le sur-échantillonnage et le filtre par filtre et un commutateur qui, à chaque échantillon, donne successivement les sorties des filtres.
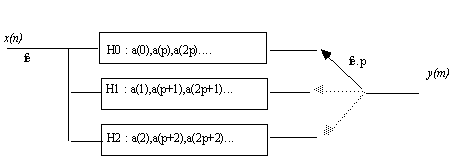
En fait, on réalise un seul filtre à coefficients variables, que l'on appelle "filtre polyphase" :
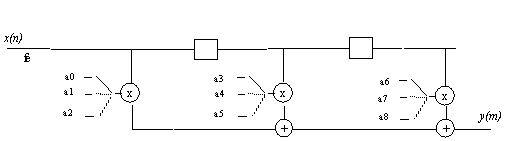
On voit que les R.I. des filtres Hi sont obtenus par échantillonnages décalés de la R.I d'un passe bas synthétisé à la fréquence de sortie.
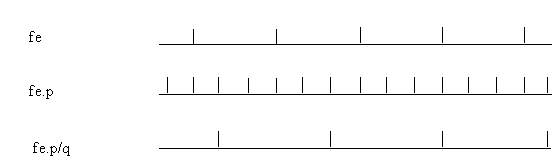
Un changement de fréquence par un facteur 
peut être considérée comme une interpolation par un facteur 
suivie d'une décimation dans un rapport 
.
On utilise pour l'interpolateur la structure de filtre à coefficients variables vue précédemment. Pour la décimation, plutôt que de calculer tous échantillons et ne garder que ceux utiles, on saute les valeurs inutiles en sautant des jeux de coefficients.
On remplace les valeurs des échantillons de sortie par celles des sorties d'un interpolateur de facteur
, en choisissant à chaque fois la date calculable la plus proche de celle qu'il faudrait. On obtient alors une structure presque identique à celle du cas fractionnaire. Le choix de facteur p détermine la précision de l'approximation. Il faut noter que sa seule limitation est la taille mémoire nécessitée par les tables de coefficients. La quantité de calcul n'est pas influencée.
Les opérations de changement de fréquence d'échantillonnage de rapport important peuvent être réalisées avantageusement par une cascade de changements de rapport plus faible. Le facteur 2 est intéressant, car il conduit à des filtres "demi-bande" particulièrement économiques puisqu'un sur deux de leurs coefficients est nul.
Les contraintes de filtrage faibles pour les premiers étages, qui peuvent être identiques. Seul le dernier étage comporte un plus grand nombre de coefficients, mais il fonctionne à fréquence plus faible.
La structure globale de l'algorithme a la propriété de nécessiter une puissance de calcul qui ne dépend que de la fréquence d'entrée, et pas du nombre de cellules.