Nous avons vu que l'échantillonnage temporel permet de transmettre un signal, de le mémoriser, et de le filtrer. Il ne suffit pas pour faire des opérations plus complexes dans le domaine des fréquences. En effet, la TFd est une fonction continue qui n'est pas manipulable en numérique. Il est donc souhaitable d'obtenir une représentation fréquentielle qui soit discrète.
Dans ce but, on peut échantillonner la TF d'un signal continu, tout comme on a échantillonné le signal temporel.
: pas d'échantillonnage en fréquence
Introduisons
Sa transformée de Fourier inverse est
|
Echantillonnage en fréquence ó Périodisation en temps. |
On peut ici énoncer une condition de Shannon duale : l'échantillonnage en fréquence est réversible si la durée du signal temporel est limitée à 
. Cela n'a guère d'application pratique.
Résumons :
Un signal de bande limitée peut être échantillonné temporellement.
Un signal de durée limitée peut être échantillonné en fréquence.
Or, un signal ne peut pas être à la fois limité en temps et en bande ! Il est donc généralement impossible d'échantillonner à la fois en temps et en fréquence.
Nous allons montrer que cela est tout de même possible que le cas d'un signal périodique.
Soit 
un signal continu périodique de période 
construit par périodisation d'un signal 
à bande limitée :
Notons que puisque
est limité en bande il n'est pas limité en durée.
La TF de est le produit d'un peigne de Dirac pas la TF de 
. Il est déjà discret en fréquence.
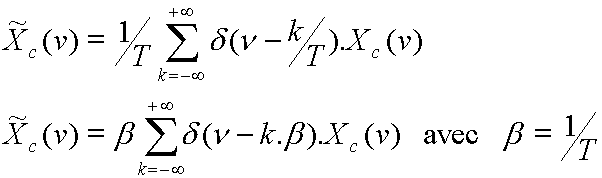
étant limité en bande, l'est aussi. Il est donc possible de l'échantillonner.
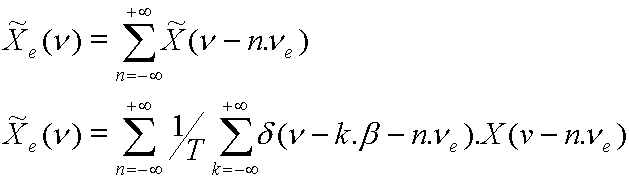
On obtient la périodisation d'une fonction multipliée par un peigne.
Si on choisit une fréquence d'échantillonnage telle qu'il y ait un nombre entier d'échantillons par période, c'est à dire tel que 
la suite discrète 
est alors périodique de période 
.
De plus, cette condition revient à écrire que
et donc 
La périodicité en fréquence est un multiple entier de l'espacement entre les impulsions de Dirac.
Avec 
périodique de période 
|
Suite périodique (N) ó Suite périodique (N) |
Établissons la relation entre ces deux suites :
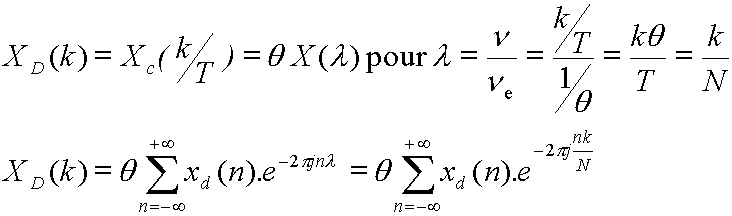
Puisque 
est périodique de période N
|
|
On obtient la relation de TFD, transformée de Fourier discrète.
La relation inverse s'établit aisément :
|
|
avec |
|
Remarque1: Ne pas confondre cette transformée de Fourier Discrète (TFD) qui fait passer d'un signal discret en temps à un signal discret en fréquence, la transformée de Fourier d'un signal discret (TFd) qui fait passer d'un signal discret en temps à un signal continue en fréquence.
Remarque2 : Ces expressions pourraient être obtenues comme une approximation numérique de la transformée de Fourier continue, en utilisant la technique d'intégration des rectangles, mais nous avons montré que cette expression est, dans les conditions ci-dessus, exacte
Remarque3 : Ces formules, avec les coefficients 
et 
ne sont pas les expressions classiques de la TFD. Il est plus habituel d'utiliser les coefficients 
et 
. L'utilisation de ces formules présente deux avantages. D'une part, comme il a été montré, la transposition du continu au discret se fait sans coefficient. D'autre part ces formules sont symétriques, ainsi que les formules dérivées du paragraphe ci-dessous, ce qui les rend plus faciles à mémoriser.
Dans les autres cas (signaux non périodiques), l'utilisation de la TDF n'est pas rigoureusement l'échantillonnage de la TF continue. Il faudra toujours avoir à l'esprit que son utilisation suppose implicitement une périodisation des signaux, et cela dans les deux espaces temps et fréquence.
Toutes les propriétés se déduisent des propriétés de la transformée continue en se rappelant que chaque signal manipulé, de durée finie, doit être considéré comme une période d'un signal périodique, et cela en temps et en fréquence. La conséquence en est que la translation d'un signal (qui intervient aussi dans les opérations de convolution ou de corrélation) se traduit par un décalage circulaire.
Soient deux signaux de durée N et leurs transformées de Fourier discrètes :
|
Linéarité |
|
|
|
Translation |
|
Figure 15 : Translation circulaire |
|
Convolution en temps |
|
Figure 16 : Convolution circulaire |
|
Convolution en fréquence |
|
|
|
Relation de Parseval |
|
|
|
Fonction de corrélation et énergie spectrale d'interaction |
|
|
On montre facilement que si 
est réel, sa transformée 
possède une symétrie Hermitienne :
Cette propriété se conserve avec la TFD.
c'est à dire 
On en déduit que 
De plus, puisque 
(périodicité)
La TFD d'un signal réel de N points peut donc se représenter par N/2+1 valeurs en partie réelle et N/2-1 valeurs en partie imaginaire (les autres de retrouvant par symétrie).
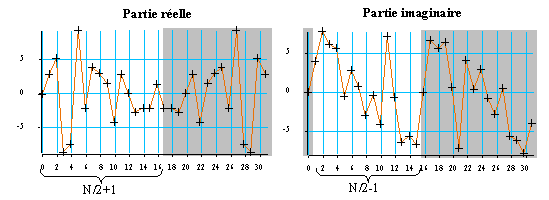
Figure 17 : TDF d'un signal réel. Seules les valeurs non grisées sont nécessaires.
